31 maret 2020

Kelas : X IPA 4, X IPS 3
kuis mtk kd 3.8
Berikut linknya

(link akan dikirim pukul 13.00)

Form di atas berupa soal pilihan ganda. Tuliskan penyelesaian jawaban kalian di buku masing2 kemudian kirim foto penyelesaian tsb beserta skor/nilai yg kalian dapat di form di atas ke email bu mira (mira.ngeblog@gmail.com)
Jgn lupa nama dan kelas
Waktu mengerjakan hanya 2 jam yakni pukul 13.00 s/d 15.00
Bagi yg tdk mengerjakan atau ketinggalan dianggap tdk mengikuti kuis.

Kelas : X IPA 3
Kegiatan hari ini:
Mencatat materi KD 3.9 "ATURAN SINUS DAN KOSINUS"

1. ATURAN SINUS

Dalam dunia trigonometri tentu kalian tidak asing dengan sinus, cosinus, dan tangen. Tahukah kalian bahwa sinus dan cosinus memiliki aturan yang khusus dan diterapkan dalam segitiga?
Lalu apa saja aturannya? Mari kita lihat penjelasan lebih lanjut dibawah ini.
 
Untuk sembarang segitiga yang sisi-sisinya a, b, dan c dengan unsur:
A = besar sudut dihadapan sisi a
a  = panjang sisi a
B = besar sudut dihadapan sisi b
b = panjang sisi b
C = besar sudut dihadapan sisi c
c = panjang sisi c
maka berlaku : Sin A= Sin B= Sin C
sehingga memenuhi Aturan Sinus :


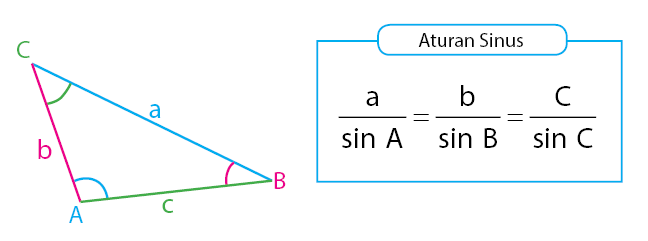
2. ATURAN KOSINUS
Aturan cosinus dapat digunakan untuk menentukan panjang salah satu sisi segitiga atau besar salah satu sudut segitiga. Persamaan yang terdapat pada aturan cosinus juga diperoleh dengan memanfaatkan fungsi trigonometri dan teorema pythagoras.


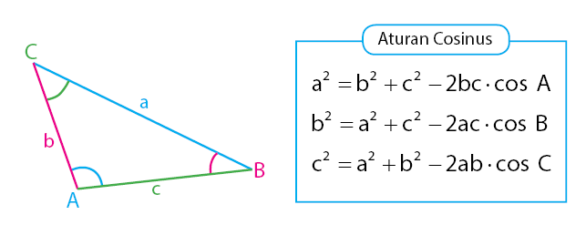
Berdasarkan tiga persamaan aturan cosinus di atas, dapat diperoleh rumus fungsi cosinus yang dapat digunakan untuk menentukan besar sudut segitiga jika diketahui panjang ketiga sisi segitiga. Persamaan fungsi cosinus tersebut dapat dilihat pada persamaan di bawah.

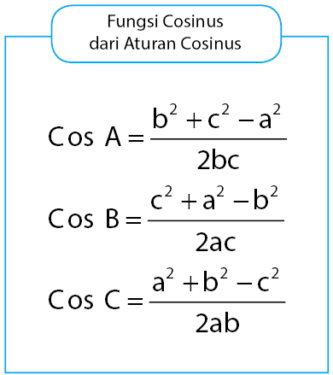
setelah kalian membaca penjelasan aturan sinus dan kosinus dapatkah kalian menentukan kapan kita harus mengerjakan suatu soal dengan menggunakan aturan sinus atau aturan kosinus???
(silahkan komen dibawah :)

30 maret 2020

Hari/tanggal : Senin/30 Maret 2020
Kelas : X IPA 6
Kegiatan :
Memperhatikan penjelasan contoh soal perbandingan trigonometri pada sudut-sudut berelasi

1.
https://youtu.be/cs3nFfWJ_BQ

2.
https://youtu.be/dT5hUCz3VPk

Pelajari contoh soal yg ada di video. Nanti diinformasikan kembali terkait kuis.

27 maret 2020

Hari/tanggal : jum'at/27 Maret 2020
Kelas : X IPA 4, X IPA 5
Kegiatan :
Memperhatikan penjelasan contoh soal perbandingan trigonometri pada sudut-sudut berelasi

1.
https://youtu.be/cs3nFfWJ_BQ

2.
https://youtu.be/dT5hUCz3VPk

Pelajari contoh soal yg ada di video. pertemuan berikutnya kita kuis.
Silahkan belajar dari referensi mana pun yang berkaitan dengan materi rasio trigonometri pada sudut-sudut berelasi

26 maret 2020

Hari/tanggal : Kamis/26 Maret 2020
Kelas : X IPA 5
Kegiatan :
Memperhatikan penjelasan contoh soal perbandingan trigonometri pada sudut-sudut berelasi

1.
https://youtu.be/cs3nFfWJ_BQ

2.
https://youtu.be/dT5hUCz3VPk

Pelajari contoh soal yg ada di video. Nanti diinformasikan kembali terkait kuis.

Kelas : X IPA 3
kuis mtk kd 3.8
Berikut linknya

https://docs.google.com/forms/d/e/1FAIpQLSc1KWpOAK6oKXt5t-9yfcA6sHz3HSshKaf9dhnW8i2oPtvaPA/viewform

Form di atas berupa soal pilihan ganda. Tuliskan penyelesaian jawaban kalian di buku masing2 kemudian kirim foto penyelesaian tsb beserta skor/nilai yg kalian dapat di form di atas ke email bu mira (mira.ngeblog@gmail.com)
Jgn lupa nama dan kelas
Waktu mengerjakan hanya 2 jam yakni pukul 13.00 s/d 15.00
Bagi yg tdk mengerjakan atau ketinggalan dianggap tdk mengikuti kuis.

25 maret 2020

Hari/tanggal : Rabu/25 Maret 2020
Kelas : X IPA 5,6 dan X IPS 3
Kegiatan :
Memperhatikan penjelasan contoh soal perbandingan trigonometri pada sudut-sudut berelasi

1.
https://youtu.be/cs3nFfWJ_BQ

2.
https://youtu.be/dT5hUCz3VPk

Pelajari contoh soal yg ada di video. Nanti diinformasikan kembali terkait kuis.

24 maret 2020

Hari /tanggal : Selasa 24 maret 2020
kelas              : X IPS 3
kegiatan        : mencatat materi rasio trigonometri pada sudut-sudut berelasi di kuadran II, III, dan IV

Sudut Berelasi di Kuadran II

Untuk α = sudut lancip, maka (90° + α) dan (180° − α) merupakan sudut-sudut kuadran II. Dalam trigonometri, relasi sudut dinyatakan sebagai berikut :
sin (90° + α) = cos α
cos (90° + α) = -sin α
tan (90° + α) = -cot α
sin (180° − α) = sin α
cos (180° − α) = -cos α
tan (180° − α) = -tan α

Sudut Berelasi Kuadran III

Untuk α = sudut lancip, maka (180° + α) dan (270° − α) merupakan sudut kuadran III. Dalam trigonometri, relasi sudut dinyatakan sebagai berikut :
sin (180° + α) = -sin α
cos (180° + α) = -cos α
tan (180° + α) = tan α
sin (270° − α) = -cos α
cos (270° − α) = -sin α
tan (270° − α) = cot α

Sudut Berelasi Kuadran IV

Untuk α = sudut lancip, maka (270° + α) dan (360° − α) merupakan sudut kuadran IV. Dalam trigonometri, relasi sudut-sudut dinyatakan sebagai berikut :
sin (270° + α) = -cos α
cos (270° + α) = sin α
tan (270° + α) = -cot α
sin (360° − α) = -sin α
cos (360° − α) = cos α
tan (360° − α) = -tan α
Ada 2 hal yang harus diperhatikan, yaitu sudut relasi yang dipakai dan tanda untuk tiap kuadran.
Untuk relasi (90° ± α) atau (270° ± α), maka :
sin → cos
cos → sin
tan → cot
Sedangkan untuk relasi (180° ± α) atau (360° ± α), maka :
sin = sin
cos = cos

tan = tan

23 maret 2020

Hari / tanggal : Senin/ 23 maret 2020
Kelas : XII IPA 1 dan XII IPA 2
Kegiatan : Latihan soal

https://docs.google.com/forms/d/e/1FAIpQLSeSgsu7mKGU8P4F-kweQabWbTYH9SFn79lFFT0ccHE_eZej-g/viewform


kelas              : X IPA 6
kegiatan        : mencatat materi rasio trigonometri pada sudut-sudut berelasi di kuadran II, III, dan IV

Sudut Berelasi di Kuadran II

Untuk α = sudut lancip, maka (90° + α) dan (180° − α) merupakan sudut-sudut kuadran II. Dalam trigonometri, relasi sudut dinyatakan sebagai berikut :
sin (90° + α) = cos α
cos (90° + α) = -sin α
tan (90° + α) = -cot α
sin (180° − α) = sin α
cos (180° − α) = -cos α
tan (180° − α) = -tan α

Sudut Berelasi Kuadran III

Untuk α = sudut lancip, maka (180° + α) dan (270° − α) merupakan sudut kuadran III. Dalam trigonometri, relasi sudut dinyatakan sebagai berikut :
sin (180° + α) = -sin α
cos (180° + α) = -cos α
tan (180° + α) = tan α
sin (270° − α) = -cos α
cos (270° − α) = -sin α
tan (270° − α) = cot α

Sudut Berelasi Kuadran IV

Untuk α = sudut lancip, maka (270° + α) dan (360° − α) merupakan sudut kuadran IV. Dalam trigonometri, relasi sudut-sudut dinyatakan sebagai berikut :
sin (270° + α) = -cos α
cos (270° + α) = sin α
tan (270° + α) = -cot α
sin (360° − α) = -sin α
cos (360° − α) = cos α
tan (360° − α) = -tan α
Ada 2 hal yang harus diperhatikan, yaitu sudut relasi yang dipakai dan tanda untuk tiap kuadran.
Untuk relasi (90° ± α) atau (270° ± α), maka :
sin → cos
cos → sin
tan → cot
Sedangkan untuk relasi (180° ± α) atau (360° ± α), maka :
sin = sin
cos = cos

tan = tan

rasio trigonometri pada sudut-sudut berelasi di kuadran II, III, dan IV

Hari/ tanggal : jumat/ 20 Maret 2020
kelas              : X IPA 4
kegiatan        : mencatat materi rasio trigonometri pada sudut-sudut berelasi di kuadran II, III, dan IV

Sudut Berelasi di Kuadran II

Untuk α = sudut lancip, maka (90° + α) dan (180° − α) merupakan sudut-sudut kuadran II. Dalam trigonometri, relasi sudut dinyatakan sebagai berikut :
sin (90° + α) = cos α
cos (90° + α) = -sin α
tan (90° + α) = -cot α
sin (180° − α) = sin α
cos (180° − α) = -cos α
tan (180° − α) = -tan α

Sudut Berelasi Kuadran III

Untuk α = sudut lancip, maka (180° + α) dan (270° − α) merupakan sudut kuadran III. Dalam trigonometri, relasi sudut dinyatakan sebagai berikut :
sin (180° + α) = -sin α
cos (180° + α) = -cos α
tan (180° + α) = tan α
sin (270° − α) = -cos α
cos (270° − α) = -sin α
tan (270° − α) = cot α

Sudut Berelasi Kuadran IV

Untuk α = sudut lancip, maka (270° + α) dan (360° − α) merupakan sudut kuadran IV. Dalam trigonometri, relasi sudut-sudut dinyatakan sebagai berikut :
sin (270° + α) = -cos α
cos (270° + α) = sin α
tan (270° + α) = -cot α
sin (360° − α) = -sin α
cos (360° − α) = cos α
tan (360° − α) = -tan α
Ada 2 hal yang harus diperhatikan, yaitu sudut relasi yang dipakai dan tanda untuk tiap kuadran.
Untuk relasi (90° ± α) atau (270° ± α), maka :
sin → cos
cos → sin
tan → cot
Sedangkan untuk relasi (180° ± α) atau (360° ± α), maka :
sin = sin
cos = cos
tan = tan

Mengerjakan soal US kelas XII

Hari/ tanggal : Kamis/19 maret 2020
Kelas : XII IPA 2
Kegiatan :
Membahas soal ujian sekolah

Rasio trigonometri pada sudut-sudut berelasi diberbagai kuadran (kuadran II, III, dan IV) kelas X

Hari/ tanggal : Kamis/ 19 Maret 2020
kelas              : X IPA 3
kegiatan        : mencatat materi rasio trigonometri pada sudut-sudut berelasi di kuadran II, III, dan IV

Sudut Berelasi di Kuadran II

Untuk α = sudut lancip, maka (90° + α) dan (180° − α) merupakan sudut-sudut kuadran II. Dalam trigonometri, relasi sudut dinyatakan sebagai berikut :
sin (90° + α) = cos α
cos (90° + α) = -sin α
tan (90° + α) = -cot α
sin (180° − α) = sin α
cos (180° − α) = -cos α
tan (180° − α) = -tan α

Sudut Berelasi Kuadran III

Untuk α = sudut lancip, maka (180° + α) dan (270° − α) merupakan sudut kuadran III. Dalam trigonometri, relasi sudut dinyatakan sebagai berikut :
sin (180° + α) = -sin α
cos (180° + α) = -cos α
tan (180° + α) = tan α
sin (270° − α) = -cos α
cos (270° − α) = -sin α
tan (270° − α) = cot α

Sudut Berelasi Kuadran IV

Untuk α = sudut lancip, maka (270° + α) dan (360° − α) merupakan sudut kuadran IV. Dalam trigonometri, relasi sudut-sudut dinyatakan sebagai berikut :
sin (270° + α) = -cos α
cos (270° + α) = sin α
tan (270° + α) = -cot α
sin (360° − α) = -sin α
cos (360° − α) = cos α
tan (360° − α) = -tan α
Ada 2 hal yang harus diperhatikan, yaitu sudut relasi yang dipakai dan tanda untuk tiap kuadran.
Untuk relasi (90° ± α) atau (270° ± α), maka :
sin → cos
cos → sin
tan → cot
Sedangkan untuk relasi (180° ± α) atau (360° ± α), maka :
sin = sin
cos = cos
tan = tan

18 maret 2020

Hari/ tanggal : Rabu/ 18 Maret 2020
kelas              : X IPA 6 dan X IPA 5
kegiatan        : mencatat materi rasio trigonometri pada sudut-sudut berelasi di kuadran I

Rumus Sudut Berelasi
Dengan memakai sudut-sudut relasi, kita mampu menghitung nilai perbandingan pada trigonometri untuk sudut pada kuadran lainnya, bahkan untuk sudut yang lebih dari 360°, termasuk juga sudut negatif.



Untuk menentukan tanda perbandingan trigonometri di setiap kuadran, ingat kembali perbandingan trigonometri pada segitiga siku-siku yang diketahui salah satu sudutnya dan sisi-sisinya berdasarkan koordinat kartesius.






tanda x  dan y didapat berdasarkan tempat kuadran sudut tersebut berada, sedangkan tanda dari r selalu positif karena merupakan hipotenusa

Sudut Berelasi di Kuadran I
Untuk α = sudut lancip, maka (90° − α) merupakan sudut-sudut kuadran I. Dalam trigonometri, relasi sudut dinyatakan sebagai berikut :
sin (90° − α) = cos α
cos (90° − α) = sin α
tan (90° − α) = cot α

contoh :


Untuk setiap perbandingan trigonometri berikut, nyatakan dalam perbandingan trigonometri sudut komplemennya !
sin 20°
tan 40°
cos 53°

Jawab :
sin 20° = sin (90° − 70°)
sin 20° = cos 70°

tan 40° = tan (90° − 50°)
tan 40° = cot 50°

cos 53° = cos (90° − 37°)
cos 53° = sin 37°

materi rasio trigonometri pada sudut-sudut berelasi diberbagai kuadran (kuadran I)

Hari/ tanggal : Selasa/ 17 Maret 2020
kelas              : X IPS 3, X IPA 3 dan X IPA 4
kegiatan        : mencatat materi rasio trigonometri pada sudut-sudut berelasi di kuadran I

Rumus Sudut Berelasi
Dengan memakai sudut-sudut relasi, kita mampu menghitung nilai perbandingan pada trigonometri untuk sudut pada kuadran lainnya, bahkan untuk sudut yang lebih dari 360°, termasuk juga sudut negatif.



Untuk menentukan tanda perbandingan trigonometri di setiap kuadran, ingat kembali perbandingan trigonometri pada segitiga siku-siku yang diketahui salah satu sudutnya dan sisi-sisinya berdasarkan koordinat kartesius.






tanda x  dan y didapat berdasarkan tempat kuadran sudut tersebut berada, sedangkan tanda dari r selalu positif karena merupakan hipotenusa

Sudut Berelasi di Kuadran I
Untuk α = sudut lancip, maka (90° − α) merupakan sudut-sudut kuadran I. Dalam trigonometri, relasi sudut dinyatakan sebagai berikut :
sin (90° − α) = cos α
cos (90° − α) = sin α
tan (90° − α) = cot α

contoh :


Untuk setiap perbandingan trigonometri berikut, nyatakan dalam perbandingan trigonometri sudut komplemennya !
sin 20°
tan 40°
cos 53°

Jawab :
sin 20° = sin (90° − 70°)
sin 20° = cos 70°

tan 40° = tan (90° − 50°)
tan 40° = cot 50°

cos 53° = cos (90° − 37°)
cos 53° = sin 37°

Jika kita perhatikan sin berubah menjadi cos, tan berubah menjadi cot dan cos berubah menjadi sin dikarenakan relasi yang digunakan adalah (90° − α) dan ketiga perbandingan trigonometri diatas bernilai positif, karena sudut 20°, 40° dan 53° berada di kuadran I.

16 maret 2020

Hari/ tanggal : senin/16 maret 2020
Kelas : XII IPA 1 dan 2
Kegiatan :
Membahas soal ujian sekolah

05 Maret 2020

Hari/tanggal :kamis /05 Maret 2020
Kelas : XII IPA 2
Kegiatan :
Bimbel UNBK membahas soal LUB

Kelas : X IPA 3, X IPA 5
Kegiatan :
Siswa memecahkan masalah tentang aplikasi trigonometri.
Berikut soal aplikasi trigonometri:


Seorang anak diminta untuk mengukur tinggi tiang listrik yang ada di depan sekolahnya dengan menggunakan klinometer. Pada posisi berdiripertama dengan melihat ujung atas tiang listrik, terlihat klinometer menunjuk sudut ${30}^{\circ }$. Kemudian dia bergerak mendekati tiang listrik sejauh $18$ m dan terlihat klinometer menunjuk sudut ${45}^{\circ }$. Tinggitiang listrik tersebut adalah $\cdots \cdot$ m.

04 maret 2020

Hari/tanggal :Rabu/04 Maret 2020
Kelas : XII IPA 1
Kegiatan :
Bimbel UNBK membahas soal LUB

Kelas : X IPA 6, X IPS 3
Kegiatan :
Siswa memecahkan masalah tentang aplikasi trigonometri.
Berikut soal aplikasi trigonometri:


Seorang anak diminta untuk mengukur tinggi tiang listrik yang ada di depan sekolahnya dengan menggunakan klinometer. Pada posisi berdiripertama dengan melihat ujung atas tiang listrik, terlihat klinometer menunjuk sudut ${30}^{\circ }$. Kemudian dia bergerak mendekati tiang listrik sejauh $18$ m dan terlihat klinometer menunjuk sudut ${45}^{\circ }$. Tinggitiang listrik tersebut adalah $\cdots \cdot$ m.

03 maret 2020

Hari/tanggal : 03 maret 2020
Kelas : XII IPA 6
Kegiatan : bimbel UNBK membahas soal LUN

Kelas : X IPS 3, X IPA 3 dan 4
Kegiatan :
Membahas soal kisi-kisi PTS materi rasio trigonometri pada sudut istimewa dan aplikasi trigonometri

02 Maret 2020

Hari/tanggal : 02 Maret 2020
Kelas : XII IPA 1 & 2
Kegiatan :
Membahas soal LUN