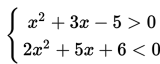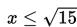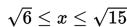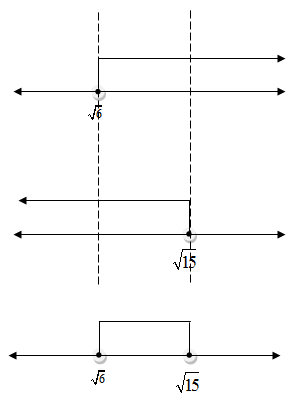Peluang Kejadian Saling Bebas, saling lepas dan peluaang kejadian bersyarat

Peluang Kejadian Saling Bebas, saling lepas dan peluaang kejadian bersyarat

Kelas               : XII IPA 1
Tanggal           : 31 Oktober 2019

KD 3.4

Mendeskripsikan dan menentukan peluang kejadian majemuk (peluang kejadian-kejadian saling bebas, saling lepas, dan kejadian bersyarat) dari suatu percobaan acak.

Kegiatan:

melanjutkan materi pda pertemuan sebelumnya yaitu peluang saling lepas dan peluang kejadian bersyarat

Kisi-kisi UB kelas X

Kegiatan :
Hari ini tgl 31 Oktober 2019 di kelas X IPA 3,4,5 dilakukan uji blok KD 3.4 dengan materi Sistem Pertidaksamaan Kuadrat 2 Variabel. Bentuk soal berupa uraian.


KD 3.4
Menjelaskan dan menentukan penyelesaian sistem pertidaksamaan dua variabel (linear-kuadrat dan kuadratkuadrat)

Berikut adalah kisi-kisi soal yang berupa uraian:
1. Diberikan dua persamaan yaitu persamaan linear dan kuadrat dan kuadrat-kuadrat. Peserta didik menentukan himpunan penyelesaian dari kedua persamaan tersebut.
2. Diberikan dua sistem persamaan yaitu persamaan linear dan kuadrat serta syarat untuk  dan  . Peserta didik menentukan hasil perkalian dari  dan
3. Diberikan dua sistem pertidaksamaan yaitu pertidaksamaan linear-kuadrat. Peserta didik menentukan daerah penyelesaian dengan menggunakan grafik.

Kisi-kisi uji blok KD 3.4 Kelas X

Kegiatan :
Hari ini tgl 31 Oktober 2019 di kelas X IPA 3,4,5 dilakukan uji blok KD 3.4 dengan materi Sistem Pertidaksamaan Kuadrat 2 Variabel. Bentuk soal berupa uraian.


KD 3.4
Menjelaskan dan menentukan penyelesaian sistem pertidaksamaan dua variabel (linear-kuadrat dan kuadratkuadrat)

Berikut adalah kisi-kisi soal yang berupa uraian:
1. Diberikan dua persamaan yaitu persamaan linear dan kuadrat dan kuadrat-kuadrat. Peserta didik menentukan himpunan penyelesaian dari kedua persamaan tersebut.
2. Diberikan dua sistem persamaan yaitu persamaan linear dan kuadrat serta syarat untuk  dan  . Peserta didik menentukan hasil perkalian dari  dan
3. Diberikan dua sistem pertidaksamaan yaitu pertidaksamaan linear-kuadrat. Peserta didik menentukan daerah penyelesaian dengan menggunakan grafik.
Sedangkan untuk kelas X IPA 5 dan 6 peserta didik mengerjakan soal latihan dengan materi persamaan dan pertidaksamaan kuadrat dua variabel. Berikut adalah soal latihannya:

kegiatan latihan pertidaksamaan kuadrat dua variabel

Materi    : Sistem Pertidaksamaan Kuadrat-Kuadrat

      Kelas      : X IPA 4, 5, 6, dan X IPS 3

      Tanggal : 29 Oktober 2019

Waktu   : 2 x 45 menit

KD 3.4

Menjelaskan dan menentukan penyelesaian sistem pertidaksamaan dua variabel (linear-kuadrat dan kuadratkuadrat)

KEGIATAN  :

Hari ini tanggal 29 Oktober 2019, kegiatan peserta didik yaitu melanjutkan latihan soal 

Peluang, frekuensi harapan, dan kejadian majemuk dan peluang komplemen

Kelas               : XII IPA 2 dan XII IPA 1
Tanggal           : 28 Oktober 2019

KD 3.4

Mendeskripsikan dan menentukan peluang kejadian majemuk (peluang kejadian-kejadian saling bebas, saling lepas, dan kejadian bersyarat) dari suatu percobaan acak.

Kegiatan hari ini :

melanjutkan materi dari pertemuan sebelumnya yaitu : peluang, frekuensi harapan, peluang komplemen suatu kejadian majemuk, dan peluang-peluang kejadian saling bebas.

Kegiatan tanya jawab siswa materi peluang kejadian saling bebas

Kegiatan :
tanya jawab siswa/i kelas XII IPA 2 materi peluang kejadian saling bebas.
Menentukan titik sampel pada pelemparan mata uang logam.

Peluang Kejadian Saling Bebas

Peluang Kejadian Saling Bebas

Kelas               : XII IPA 2
Tanggal           : 25 Oktober 2019

KD 3.4

Mendeskripsikan dan menentukan peluang kejadian majemuk (peluang kejadian-kejadian saling bebas, saling lepas, dan kejadian bersyarat) dari suatu percobaan acak.

Kegiatan:

Berdiskusi mengingat kembali peluang suatu kejadian.

Mengamati

Berikut adalah percobaan dalam statistika. Lengkapilah tabel berikut:

No	Percobaan	Titik Sampel
1	Pelemparan sekeping mata uang logam	...
2	Pelemparan dua keping mata uang logam secara bersamaan	...
3	Pelemparan sebuah dadu	...
4	Pelemparan dua buah dadu bersamaan	...
5	Pelemparan sekeping mata uang logam dan sebuah dadu	...
6	Pelemparan mata uang logam sebanyak 50 kali	...

Mengkomunikasikan

Berdasarkan tabel di atas, jawablah pertanyaan berikut:

a.    Disebut apakah kejadian munculnya mata dadu satu pada pelemparan sebuah dadu?

b.    Disebut kejadian apakah kejadian munculnya minimal satu gambar pada pelemparan dua keping mata uang logam?

c.    Berdasarkan kegiatan yang telah dilakukan dapat disimpulkan bahwa peluang suatu kejadian saling bebas adalah?

Persentasikan hasil diskusi di depan kelas.

Peluang Suatu Kejadian

Materi    :Kaidah Pencacahan

      Kelas      : XII IPA 2  dan 1

      Tanggal : 24 Oktober 2019

Waktu   : 2 x 45 menit

Pada artikel kali ini kalian akan belajar tentang percobaan, ruang sampel dan peluang menghitung  suatu kejadian. Kita bahas satu-persatu ya. Sebelumnya tentu kalian sudah membaca kan? Tentang kombinasi dan binomial Newton? Nah, ini pembahasan lanjutannya. Yuk, kita simak bersama-sama!

A. Percobaan

Sifat dasar percobaan:

1. Setiap jenis percobaan mempunyai kemungkinan hasil atau peristiwa/kejadian yang akan terjadi.
2. Hasil dari setiap percobaan secara pasti sulit ditentukan.

B. Ruang Sampel
Ruang sampel (S) adalah kumpulan dari hasil yang mungkin terjadi dari suatu percobaan.  Titik sampel adalah anggota-anggota dari ruang sampel, sedangkan kumpulan dari beberapa titik sampel disebut kejadian.
Banyak ruang sampel disimbolkan dengan n(S).
Contoh:
Sebuah koin di lempar sebanyak 3 kali, maka ruang sampel dan banyaknya sampel dari percobaan pelemparan koin tersebut adalah ...
Jawab:
Kemungkinan
Koin ke-1 : A A A G A G G G
Koin ke-2 : A A G A G A G G
Koin ke-3 : A G A A G G A G
S = {(AAA), (AAG), (AGA), (GAA), (AGG), (GAG), (GGA), (GGG)}
n(S) = 8

C. Peluang Kejadian
Misalnya S adalah ruang sampel dari suatu percobaan dengan setiap anggota S memiliki kesempatan muncul yang sama dan K adalah suatu kejadian dengan K⊂S, maka peluang kejadian K adalah:

Contoh:
Sebuah dadu dilempar undi satu kali, peluang muncul angka bilangan prima adalah...
Jawab:
Ruang sampel dadu (S) = {1, 2, 3, 4, 5, 6}  maka n(S) = 6
Muncul angka prima (K) = {2, 3, 5} maka n(K) = 3
Sehingga peluang muncul angka bilangan prima yaitu:

D. Peluang komplemen dari suatu kejadian

P(K) adalah peluang kejadian K dan P(Kc) = P(K’) adalah peluang kejadian bukan K, maka berlaku:

Contoh:
Peluang Rina lulus ujian Matematika adalah 0,89, maka peluang Rina tidak lulus ujian Matematika adalah…
Jawab:
K = Kejadian Rina lulus ujian Matematika = 0,89
Kc = Kejadian Rina tidak lulus ujian Matematika
Peluang Rina tidak lulus ujian Matematika:
P(Kc) = 1 – P(K) = 1 – 0,89 = 0,11

E. Frekuensi Harapan

Frekuensi  harapan adalah banyaknya kejadian yang diharapkan dapat terjadi pada suatu percobaan.

Jika suatu percobaan dilakukan sebanyak n kali dan nilai kemungkinan terjadi kejadian K setiap percobaan adalah P(K), maka frekuensi harapan kejadian K adalah:

Contoh:
Sebuah dadu dilempar sebanyak 120 kali, maka frekuensi harapan munculnya mata dadu faktor dari 6 adalah...
Jawab:
S = {1, 2, 3, 4, 5, 6} ↔ n(S) = 6
K : Faktor dari 6 = {1, 2, 3, 6} ↔ n(A) = 4
n = Banyak lemparan = 120

Sehingga frekuensi harapan muncul faktor dari 6 adalah :

Sistem Pertidaksamaan Kuadrat-Kuadrat

Materi    : Sistem Pertidaksamaan Kuadrat-Kuadrat

      Kelas      : X IPA 3, 6, dan X IPS 3

      Tanggal : 23 Oktober 2019

Waktu   : 2 x 45 menit

Model Matematika Sistem Pertidaksamaan Kuadrat Dua Variabel

Pada topik sebelumnya kita telah mempelajari konsep pertidaksamaan kuadrat dua variabel. Dalam topik ini kita akan mempelajari model matematika sistem pertidaksamaan kuadrat dua variabel.
Sebelum kita memulai topik model matematika sistem pertidaksamaan kuadrat dua variabel, marilah kita mengingat kembali konsep dari sistem pertidaksamaan kuadrat dua variabel.

Sistem Pertidaksamaan kuadrat dua variabel
Pertidaksamaan kuadrat dua variabel merupakan pertidaksamaan yang memuat dua variabel dengan pangkat tertinggi dua.
Contoh bentuk umum pertidaksamaan kuadrat dua variabel

Apakah kalian sudah ingat kembali? Jika sudah, mari kita pelajari model matematika sistem Pertidaksamaan kuadrat dua variabel

Model Matematika Sistem Pertidaksamaan Kuadrat Dua Variabel

Langkah – langkah dalam menyelesaikan model matematika sistem pertidaksamaan kuadrat dua variabel yaitu :
1. Mencari kata – kata seperti “ kurang dari”(<), “lebih dari”(>), “tidak lebih dari”(≤), tidak kurang dari”(≥).
2. Setelah menemukan kata – kata tersebut merumuskan model matematika dari masalah
3. Menentukan penyelesaian dari model matematika
4. Memberikan penafsiran dari hasil yang didapat
Agar lebih memahami marilah kita mencermati contoh dibawah ini
Contoh:
Panjang dan lebar dari persegi panjang ABCD masing – masing 30 cm dan 20 cm bagian tepi persegi panjang tersebut dipotong selebar x2 sehingga diperoleh persegi panjang PQRS. Jika keliling persegi panjang PQRS tidak kurang dari 52 cm maka tentukan batas – batas x yang dapat dilakukan.
Penyelesaian:
Misal panjang persegi panjang PQRS = 30- 2x2 , lebar persegi panjang PQRS = 20 – 2x2
Keliling persegi panjang PQRS ≤ 52
2( p + l) ≤ 52
2(30 – 2x2 + 20 -2x2 ) ≤ 52
2( 50 – 4x2 ) ≤ 52
100 – 8x2 ≤ 52
-8x2 ≤ 52 -100
8x2 ≥ 48
x2 ≥ 6

Panjang persegi panjang PQRS ≥ 0
30 – 2x2 ≥ 0
-2x2 ≥ - 30
2x2 ≤ 30
x2 ≤ 15

Batas – batas yang dapat dilakukan

Sistem Pertidaksamaan Kuadrat-Kuadrat

Materi    : Sistem Pertidaksamaan Linear-Kuadrat

      Kelas      : X IPA 3, 6, dan X IPS 3

      Tanggal : 22 Oktober 2019

Waktu   : 2 x 45 menit

Model Matematika Sistem Pertidaksamaan Kuadrat Dua Variabel

Pada topik sebelumnya kita telah mempelajari konsep pertidaksamaan kuadrat dua variabel. Dalam topik ini kita akan mempelajari model matematika sistem pertidaksamaan kuadrat dua variabel.
Sebelum kita memulai topik model matematika sistem pertidaksamaan kuadrat dua variabel, marilah kita mengingat kembali konsep dari sistem pertidaksamaan kuadrat dua variabel.

Sistem Pertidaksamaan kuadrat dua variabel
Pertidaksamaan kuadrat dua variabel merupakan pertidaksamaan yang memuat dua variabel dengan pangkat tertinggi dua.
Contoh bentuk umum pertidaksamaan kuadrat dua variabel

Apakah kalian sudah ingat kembali? Jika sudah, mari kita pelajari model matematika sistem Pertidaksamaan kuadrat dua variabel

Model Matematika Sistem Pertidaksamaan Kuadrat Dua Variabel

Langkah – langkah dalam menyelesaikan model matematika sistem pertidaksamaan kuadrat dua variabel yaitu :
1. Mencari kata – kata seperti “ kurang dari”(<), “lebih dari”(>), “tidak lebih dari”(≤), tidak kurang dari”(≥).
2. Setelah menemukan kata – kata tersebut merumuskan model matematika dari masalah
3. Menentukan penyelesaian dari model matematika
4. Memberikan penafsiran dari hasil yang didapat
Agar lebih memahami marilah kita mencermati contoh dibawah ini
Contoh:
Panjang dan lebar dari persegi panjang ABCD masing – masing 30 cm dan 20 cm bagian tepi persegi panjang tersebut dipotong selebar x2 sehingga diperoleh persegi panjang PQRS. Jika keliling persegi panjang PQRS tidak kurang dari 52 cm maka tentukan batas – batas x yang dapat dilakukan.
Penyelesaian:
Misal panjang persegi panjang PQRS = 30- 2x2 , lebar persegi panjang PQRS = 20 – 2x2
Keliling persegi panjang PQRS ≤ 52
2( p + l) ≤ 52
2(30 – 2x2 + 20 -2x2 ) ≤ 52
2( 50 – 4x2 ) ≤ 52
100 – 8x2 ≤ 52
-8x2 ≤ 52 -100
8x2 ≥ 48
x2 ≥ 6

Panjang persegi panjang PQRS ≥ 0
30 – 2x2 ≥ 0
-2x2 ≥ - 30
2x2 ≤ 30
x2 ≤ 15

Batas – batas yang dapat dilakukan

LATIHAN KOMBINASI

Materi    :Kaidah Pencacahan

      Kelas      : XII IPA 2  dan 1

      Tanggal : 21 Oktober 2019

Waktu   : 2 x 45 menit

Latihan Soal Permutasi

Materi    :Kaidah Pencacahan

      Kelas      : XII IPA 2

      Tanggal : 18 Oktober 2019

Waktu   : 2 x 45 menit

Kerjakan Soal berikut dengan baik dan benar!