LKPD MTK WAJIB KELAS 10

Materi Ajar Persamaan dan Pertidaksamaan Nilai Mutlak Kelas X Matematika Wajib

MATERI AJAR (Persamaan dan Pertidaksamaan Nilai Mutlak)

KD 3.1

Mengintepretasi persamaan dan pertidaksamaan nilai mutlak dari bentuk linear satu variabel dengan persamaan dan pertidaksamaan linear Aljabar lainnya.

IPK

3.1.1           Menentukan himpunan penyelesaian persamaan nilai mutlak linear satu variabel

3.1.2           Menentukan himpunan penyelesaian pertidaksamaan nilai mutlak linear satu variabel

Tujuan Pembelajaran

Melalui kegiatan pembelajaran menggunakan model discovery learning yang dipadukan melalui pendekatan saintifik yang menuntut peserta didik untuk dapat mengintepretasi persamaan dan pertidaksamaan nilai mutlak dari bentuk linear satu variabel dengan persamaan dan pertidaksamaan linear aljabar lainnya. . Selain itu, peserta didik dapat menyelesaikan masalah yang berkaitan dengan persamaan dan pertidaksamaan nilai mutlak dari bentuk linear satu variable dengan rasa rasa ingin tahu, tanggung jawab, displin selama proses pembelajaran, bersikap jujur, disiplin, santun, peduli (gotong royong, kerjasama, toleran, damai), bertanggung jawab, responsif, dan pro-aktif dalam berinteraksi, serta mampu berkomukasi dan bekerjasama dengan baik.

 

Menyelesaikan Persamaan Mutlak

Nilai mutlak suatu bilangan dapat diartikan jarak antara bilangan tersebut dari titik nol(0). Dengan demikian jarak selalu bernilai positif.
Misalnya:
Parhatikan garis bilangan berikut.

 





Jarak angka 5 dari titik 0 adalah 5
Jarak angka -5 dari titik 0 adalah 5
 

Dari penjelesan di atas memang tampak bahwa nilai mutlak suatu bilangan selalu bernilai positif. 
Berkaitan dengan menentukan nilai mutlak suatu bilangan, maka muncullah tanda mutlak. Tanda mutlak disimbolkan dengan  garis 2 ditepi suatu bilangan atau bentuk aljabar.
Misalnya seperti berikut.

Secara umum, bentuk persamaan nilai mutlak dapat dimaknai seperti berikut.

Sifat dari nilai mutlak :

Sifat 1. Untuk x∈R, a∈R dan a>0
i) |𝒙| ≤ 𝒂 ⟺ -𝒂 ≤ 𝒙 ≤ 𝒂

ii) |𝒙| ≥ 𝒂 ⟺ 𝒙 ≤ -𝒂  atau 𝒙 ≥ 𝒂

Sifat 2.
        

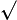
Sifat 3. Untuk x∈R, y∈R dan y≠0
i) |𝒙𝒚|=|𝒙||𝒚|

ii)        

iii) |𝒙 + 𝒚| ≤ |𝒙| + |𝒚|

iv) |𝒙 - 𝒚| ≥ |𝒙| - |𝒚|

Contoh 
Tentukan himpunan penyelesaian dari persamaan nilai Mutlak di bawah ini.

Jawaban:
Bentuk-Bentuk persamaan nilai mutlak di atas dapat diselesaikan sebagai berikut. Pada prinsipnya, langkah langkah penyelesaian nilai mutlak diusahakan bentuk mutlak berada di ruas kiri. 
1. Pada bentuk ini ada dua penyelesaian.
   (*) x + 5 = 3  , maka  x = 3 - 5 = -2
   (**) x + 5 = -3, maka x = -3 - 5 = -8
  Jadi, himpunan penyelesaiannya adalah {-2, -8}

2.  Pada bentuk ini ada dua penyelesaian.
   (*) 2x + 3 = 5  , maka  2x = 5 - 3 
                                       2x = 2  <==>  x = 1
   (**) 2x + 3 = -5  , maka  2x = -5 -3
                                         2x = -8  <==> x = -4
  Jadi, himpunan penyelesaiannya adalah {-4, 1}

3. Perhatikan bentuk aljabar di dalam tanda mutlak, yaitu x+1.Penyelesaian persamaan nilai mutlak ini juga dibagi menjadi dua bagian.
Bagian pertama untuk batasan x+1>= 0 atau x >= -1

Bagian kedua untuk batasan x+1< 0 atau x < -1
Mari kita selesaikan.
(*) untuk x >=-1
     Persamaan mutlak dapat ditulis:
    (x + 1) + 2x = 7
                   3x = 7 - 1
                   3x = 6
                     x = 2 (terpenuhi, karena batasan >= -1)

(**) untuk x < -1
     Persamaan mutlak dapat ditulis:
    -(x + 1) + 2x = 7
        -x - 1 + 2x = 7
                      x = 7 + 1                 
                      x = 8 (tidak terpenuhi, karena batasan < -1)

Jadi, Himpunan penyelesaiannya adalah {2}.

 4.  
Perhatikan bentuk aljabar di dalam tanda mutlak, yaitu 3x + 4. Penyelesaian persamaan nilai mutlak ini juga dibagi menjadi dua bagian.
Bagian pertama untuk batasan 3x+4>= 0 atau x >= -4/3

Bagian kedua untuk batasan 3x+4< 0 atau x < -4/3
Mari kita selesaikan.
(*) untuk x >=-4/3
     Persamaan mutlak dapat ditulis:
    (3x + 4) = x - 8
        3x - x = -8 - 4
             2x =-12
               x = -6 (tidak terpenuhi, karena batasan >= -4/3)
(**) untuk x < -4/3
     Persamaan mutlak dapat ditulis:
    -(3x + 4) = x - 8
        -3x - 4 = x -8
         -3x - x = -8 + 4 
              -4x = -4
                 x = 1 (tidak terpenuhi, karena batasan < -4/3)

Jadi, Tidak ada Himpunan penyelesaiannya.

Menyelesaikan Pertidaksamaan Nilai Mutlak
Menyelesaikan pertidaksamaan nilai mutlak caranya hampir sama dengan persamaan nilai mutlak. hanya saja berbeda sedikit pada tanda ketidaksamaannya. Langkah-langkah selanjutnya seperti menyelesaikan pertidaksamaan linear atau kuadrat satu variabel .
Pertidaksamaan  mutlak dapat digambarkan sebagai berikut.

Apabila fungsi di dalam nilai mutlak berbentuk ax + b maka pertidaksamaan nilai mutlak dapat diselesaikan seperti berikut.



Lebih jelasnya perhatikan contoh berikut ini.

Contoh
Tentukan himpunan penyelesaian dari Pertidaksamaan nilai mutlak berikut ini.

Jawaban
1.Cara menyelesaikan pertidaksamaan mutlak ini sebagai berikut.
    -9 < x+7 < 9
    -9 - 7 < x < 9 - 7
       -16 < x < 2
   Jadi, himpunan penyelesaiannya adalah { x/ -16 < x < 2}

2. Cara menyelesaikan pertidaksamaan mutlak ini dibagi menjadi dua bagian.
   (*) 2x - 1 >=  7
             2x  >=  7 + 1
             2x  >= 8
               x  >= 4

  (**) 2x - 1 <= -7
             2x   <= -7 + 1
             2x   <= -6
               x   <= -3

    Jadi, himpunan penyelesaiannya adalah { x/ x <= -3 atau x >= 4}

 3. Kalau dalam bentuk soal ini, langkah menyelesaikan pertidaksamaannya dengan mengkuadratkan kedua ruas.
perhatikan proses berikut ini.

(x + 3)² <= (2x – 3)²

(x + 3)² - (2x – 3)² <= 0

(x + 3 + 2x – 3) (x + 3 – 2x + 3) <= 0 (ingat: a² – b² = (a+b)(a-b))

x (6 - x) <=0

Pembuat nol adalah x = 0 dan x = 6

Mari selidiki menggunakan garis bilangan

Oleh karena batasnya <= 0, maka penyelesaiannya adalah x <=0 atau x >=6.

Jadi, himpunan penyelesaiannya adalah {x/ x <= 0 atau x >= 6}.

Mari selidiki menggunakan garis bilangan

Oleh karena batasnya <= 0, maka penyelesaiannya adalah x <=0 atau x >=6.

Jadi, himpunan penyelesaiannya adalah {x/ x <= 0 atau x >= 6}.

4. Menyelesaikan pertidaksamaan nilai mutlak seperti ini lebih mudah menggunakan cara menjabarkan definisi.
Prinsipnya adalah batasan-batasan pada fungsi nilai mutlaknya.
Perhatikan pada 3x + 1 dan 2x + 4.

Dari batasan batasan itu maka dapat diperoleh batasan-batasan nilai penyelesaian seperti pada garis bilangan di bawah ini.

Dengan garis bilangan tersebut maka pengerjaanya dibagi menjadi 3 bagian daerah penyelesaian.
1. Untuk batasan x >= -1/3  ......(1)
   (3x + 1) - (2x + 4) < 10
          3x + 1 - 2x- 4 < 10
                         x- 3 < 10
                             x < 13 .......(2)

  Dari (1) dan (2) diperoleh irisan penyelesaian -1/3 <= x < 13

2. Untuk batasan -2<= x < -1/3  ......(1)
    -(3x + 1) - (2x + 4) < 10
          -3x - 1 - 2x - 4 < 10
                       -5x - 5 < 10
                             -5x < 15 
                               -x < 3
                             x > 3 .......(2)

  Dari (1) dan (2) tidak diperoleh irisan penyelesaian atau tidak ada penyelesaian.

3. Untuk batasan x < -2  ......(1)
   -(3x + 1) + (2x + 4) < 10
         -3x - 1 + 2x + 4 < 10
                        -x + 3 < 10
                             -x  < 7 
                                x > -7 .......(2)

  Dari (1) dan (2) diperoleh irisan penyelesaian -7 < x < -2.

Jadi, himpunan penyelesaiannya adalah {x/ -1/3 <= x < 13 atau -7 < x < -2}

Sumber :
Buku Siswa Matematika untuk SMA/MA/SMK Kelas X (Wajib) penerbit CV Mediatama Tahun 2018
https://yos3prens.wordpress.com/2013/11/17/menyelesaikan-persamaan-nilai-mutlak/

https://takadadikotomi.blogspot.com/2018/07/nilai-mutlak-dan-sifat-sifatnya.html